Question

Analyze the function f(x) = - 2 cot 3x. Include: - Domain and range - Period - Two Vertical Asymptotes (6 points) HTML EditorKeyboard Shortcuts

Answer 1

Domain: All values (-∞,+∞) except x =
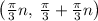`\left((\pi )/(3)n,\:(\pi )/(3)+(\pi )/(3)n\right)` for all real integers.

Range: (-inf, inf)

Period: pi/3

Vertical Asymptotes: n*pi/3 for all real values of n

Explanation:

Domain

• For domain we equate the denominator of the equivalent fraction to zero and solve for x.
• Denominator: sin (3x) = 0
• Solve for x
• x = (…, -2*pi/3, - pi/3, 0, pi/3, 2*pi/3,…)
• Hence we can condense the domain based on a pattern as follows:

x = are all values from - infinity to + infinity except x =
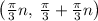`\left((\pi )/(3)n,\:(\pi )/(3)+(\pi )/(3)n\right)` for all values of n

Range

• What are the values the function outputs when its defined as per domain above.

• input the end-points of the domain in f(x) evaluated above:
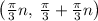  `\left((\pi )/(3)n,\:(\pi )/(3)+(\pi )/(3)n\right)` for all values of n.

• Now solve for x = 0 , y = ? and x = pi/3, y = ?
• We see the denominator approaches 0 at end points hence entire function approaches -∞ and ∞ !

Hence, Range = (-∞,∞)

Period

• The period of a cotangent function can be evaluated by a formula as follows:
• f(X) = a cot (bx)
• Period = Pi / modulus (b)
• Hence, from the given function we can evaluate accordingly as follows:

Period = Pi / 3

Vertical Asymptotes:

• Vertical Asymptotes exist for rational fractions and logarithms only.
• For values of x for which a fraction is undefined are denoted as vertical asymptotes as we scrutinize on the denominator.
• In our case, values of x when sin (3x) = 0
• From the part of domain evaluated above we got pi*n/3 for all values of n.

Hence, our two vertical asymptotes can be x = 0 and x = pi/3 with n = 0 and n = 1, respectively. Other possibilities can be evaluated by using other real values for n.