Question

A student has a weight of 655 N. While riding a roller coaster they seem to weigh 1.96x 103 N at the bottom of a dip that has a radius of 18.0 m. What is the speed of the roller coaster at this point?

Answer 1

Step-by-step explanation:

weight, mg = 655 N

m = 655 / 9.8 = 66.84 Kg

N = 1.96 x 10^3 N

radius, r = 18 m

Let v be the speed of roller coaster.

So, the apparent weight

N = mg + mv²/r

1.96 x 1000 = 655 + 66.84 v² / 18

1305 = 3.71 v²

v² = 351.75

v = 18.76 m/s

Answer 2

The speed of the roller coaster at this point is 18.74 m/s.

Step-by-step explanation:

Given that,

Weight of the student, W = 655 kg

Weight of the roller coaster,
`F=1.96* 10^3\ N`

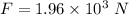
Radius of the roller coaster, r = 18 m

At the bottom of the loop, the weight of the roller coaster us given by :

`F=W+(mv^2)/(r)`

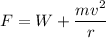
If m is the mass of the roller coaster,

`W=mg`

`m=(W)/(g)`

`m=(655)/(9.8)`

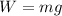
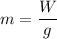
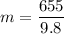
m = 66.83 kg

So,

`F=W+(mv^2)/(r)`

`v=\sqrt{((F-W)r)/(m)}`

`v=\sqrt{((1.96* 10^3-655)* 18)/(66.83)}`

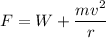
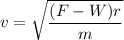
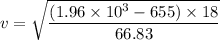
v = 18.74 m/s

So, the speed of the roller coaster at this point is 18.74 m/s. Hence, this is the required solution.