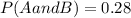Question

P(A) = 0.7 P(A and B) = 0.21 P(B\A) =

Answer 1

1) Conditional probability
`P(B/A)=0.3`

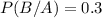
2)
`P(A and B)=0.28`

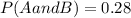
Explanation:

1) Given that P(A)=0.7 and P(A and B)=0.21

To find the conditional probability :

Conditional probability
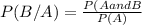`P(B/A)=(P(A and B)/(P(A))` when P(A)>0

Substitute the values P(A)=0.7 and P(A and B)=0.21 in above formula we get

`P(B/A)=(0.21)/(0.7)</p><p>[tex]=0.3`

Therefore
`P(B/A)=0.3`

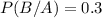
Therefore the Conditional probability
`P(B/A)=0.3`

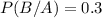
2) Given that P(A)=0.4 and P(B)=0.7 and also given that Events A and B are independents

To find P(A and B) :

`P(A and B)=P(A)* P(B)`

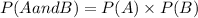
Substitute the values P(A)=0.4 and P(B)=0.7 in above formula we get

`P(A and B)=(0.4)* (0.7)`

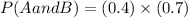
=0.28[/tex]

Therefore
`P(A and B)=0.28`