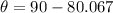Question

Find x, the angle of depression from the top of a lighthouse that is 152ft above water level to the waterline of a ship 868ft off shore. Round your answer to the nearest hundredth of a degree.

Answer 1

`\theta = 9.93`

Explanation:

If we draw a right angle triangle ABC,

where B is the vertex with 90 degrees.

A is the top of the lighthouse

C is the waterline of the ship.

we can write the sidelengths of this triangle.

AB = 152

BC = 868.

to find the angle of depression
`(\theta)`, all we need to find is the angle BAC and subtract it from 90 degrees.

`\theta = 90 - B\hat{A}C`

to find the angle BAC, we'll use trigonometric functions.

we don't have the hypotenuse of the triangle, and we won't be needing it either. we'll use tan

`tan(x) = \frac{\text{opposite side}}{\text{adjacent side}}`

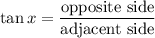
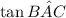`\tan{B\hat{A}C`} = \dfrac{BC}{AB}[/tex]

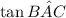`\tan{B\hat{A}C`} = \dfrac{868}{152}[/tex]

`B\hat{A}C = \arctan{\left((868)/(152)\right)}`

`B\hat{A}C = 80.067`

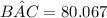
to find the angle of depression:

`\theta = 90 - B\hat{A}C`

`\theta = 90 - 80.067`

`\theta = 9.93`