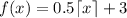Question

Please help thx in adv

Answer 1

Given function:

`\implies f(x)=(100)/(1+80e^(-0.3x))`

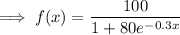
y-intercept is when x = 0:

`\implies f(0)=(100)/(1+80e^(-0.3\cdot0))`

`\implies f(0)=(100)/(81)=1.23 \ \sf(2 \ dp)`

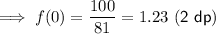
Asymptotes:

y = 0

y = 100

Therefore, upper asymptote is y = 100

The function is in the form of the logistic growth model:

`f(x)=(c)/(1+ae^(-bx))`

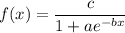
The point of maximum growth is
`\left((\ln(a))/(b),(c)/(2) \right)`

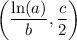
Given:

• a = 80
• b = 0.3
• c = 100

Therefore, point of maximum growth is:

`\implies \left((\ln(80))/(0.3),(100)/(2) \right)`

`\implies (14.61, 50)`

---------------------------------------------------

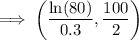
f(x) = 4 | x | - 1

y-intercept (0, -1)

x-intercepts: (-0.25, 0) (0.25, 0)

`f(x)=0.5 \lceil x \rceil+3`