a) The slopes of the secant lines are listed below:
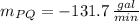
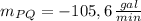
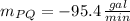
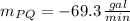
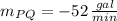
b) The slope of the tangent line is approximately -100.5 gallons per minute.
Application of secant and tangent line in a water tank draining process
a) The value of the slope of line secant (
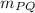 ) to a curve is defined by the following expression:
) to a curve is defined by the following expression:
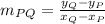 , where
, where
 (1)
(1)
Now we proceed to calculate for each case:
i)
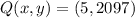
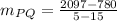
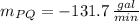

ii)
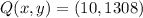
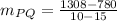
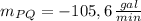

iii)
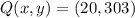
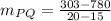
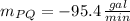

iv)
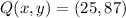

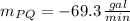

v)
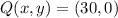
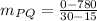
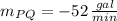

ii) The slope of the tangent line at P can be estimated by the following formula:
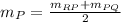 (2)
(2)
Where
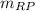 and
and
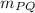 are secant lines.
are secant lines.
If we know that
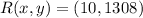 ,
,
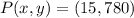 and
and
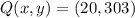 , then the slope of tangent line is:
, then the slope of tangent line is:
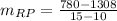

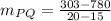

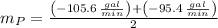
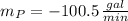
The slope of the tangent line is approximately -100.5 gallons per minute.

Remark
The statement is incomplete and poorly formatted, the complete and correct form is described below:
A tank holds 3000 gallons of water, which drains from the bottom of the tank in half an hour. The values in the table show the volume
 of water remaining in the tank (in gallons) after
of water remaining in the tank (in gallons) after
 minutes.
minutes.
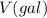
5 2097
10 1308
15 780
20 303
25 87
30 0
(a) If
 is the point (15, 780) on the graph of
is the point (15, 780) on the graph of
 , find the slopes of the secant lines
, find the slopes of the secant lines
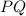 when
when
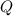 is the point on the graph with the following values. (Round your answers to one decimal place)
is the point on the graph with the following values. (Round your answers to one decimal place)
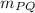
(5, 2097)
(10, 1308)
(20, 303)
(25, 87)
(30, 0)
(b) Estimate the slope of the tangent line
 by averaging the slopes of two adjacent secant lines. (Round your answer to one decimal place)
by averaging the slopes of two adjacent secant lines. (Round your answer to one decimal place)