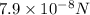Question

In the Bohr model of the hydrogen atom, an electron moves in a circular path around a proton. The speed of the electron is approximately 2.15 106 m/s?

Answer 1

This is an incomplete question, here is a complete question.

In the Bohr model of the hydrogen atom, an electron moves in a circular path around a proton. The speed of the electron is approximately
`2.15* 10^6m/s`?

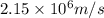Find the force acting on the electron as it revolves in a circular orbit of radius
`5.34* 10^(-11)m`.

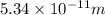Answer : The force acting on electron is,
`7.9* 10^(-8)N`

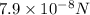
Explanation :

Formula used :

`F=(mv^2)/(r)`

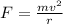
where,

F = force acting on electrons

m = mass of electrons =
`9.1* 10^(-31)kg`

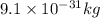
v = speed of electron =
`2.15* 10^6m/s`

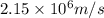
r = radius of circular orbit =
`5.34* 10^(-11)m`

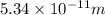
Now put all the given values in the above formula, we get:

`F=((9.1* 10^(-31)kg)* (2.15* 10^6m/s)^2)/(5.34* 10^(-11)m)`

`F=7.9* 10^(-8)N`

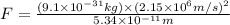
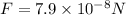
Thus, the force acting on electron is,
`7.9* 10^(-8)N`