Answer: A.) Lines 2 and 4 are perpendicular
Explanation:
Two lines are said to be perpendicular if the product of their slope gives - 1 . That is , if
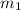 is the slope of the first line and
is the slope of the first line and
 is the slope of the second line , if the two lines are perpendicular , then :
is the slope of the second line , if the two lines are perpendicular , then :
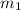
 = -1 , which can also be written as ;
= -1 , which can also be written as ;
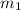 = -1 /
= -1 /
 .
.
The equation of line in slope intercept form is given as :
y = mx + c , where m is the slope and c is the y - intercept.
Line one : y = - 1 , comparing with the equation of line in slope intercept form , it means line one has no slope
Line two : y = -1/2x - 2 , it has a slope of - 1/2
Line 3 : x = -4 , has no slope
Line 4 : y + 3 = 2 ( x - 2 )
Writing this in slope intercept form , we will make y the subject of the formula.
y + 3 = 2x - 4
y = 2x -4 - 3
y = 2x - 7
This means that the slope of line 4 is 2.
Comparing line two and line four to check if they are perpendicular
- 1/2 x 2 = - 1 , surely , it obeys the perpendicularity rule , this means that line 2 and 4 are perpendicular