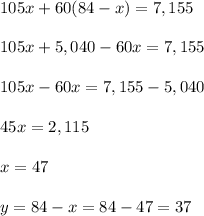Question

a local dinner theater sells adult tickets for $105 and each children tickets for $ 60 each. for a certain show the theater sells 84 tickets for a total of 7,155. how many of each type of ticket were sold. define the variables for this problem​ please hurry thank you

Answer 1

The theater sells 47 adult tickets and 37 children tickets

Explanation:

Let

x = number of adult tickets sold

y = number of children tickets sold

1. A local dinner theater sells adult tickets for $105 each, then they get $105x selling x adult tickets and each children tickets for $60 each, then they get $60y selling y children tickets.

They make a total of $7,155, so

`105x+60y=7,155`

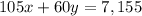
2. In total, the theater sells 84 tickets, so

`x+y=84`

3. Express y from the second equation

`y=84-x`

and substitute it into the first equation:

`105x+60(84-x)=7,155\\ \\105x+5,040-60x=7,155\\ \\105x-60x=7,155-5,040\\ \\45x=2,115\\ \\x=47\\ \\y=84-x=84-47=37`