Question

The fastest server in women's tennis is Venus Williams, who recorded a serve of 204 km/h at the French Open in 2007. Suppose that the mass of her racket was 331g and the mass of the ball was 56.0g. If her racket was moving at 200 km/h when it hit the ball, approximately what was the racket's speed after hitting the ball?

Answer 1

45.96844 m/s

Step-by-step explanation:

`m_1` = Mass of racket = 331 g

`m_2` = Mass of ball = 56 g

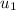`u_1` = Initial velocity of racket = 200 km/h

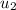`u_2` = Initial velocity of ball = 0

`v_1` = Final velocity of racket

`v_2` = Final velocity of ball = 204 km/h

In this system the linear momentum is conserved

`m_1u_1+m_2u_2=m_1v_1+m_2v_2\\\Rightarrow v_1=(m_1u_1+m_2u_2-m_2v_2)/(m_1)\\\Rightarrow v_1=(0.331* (200)/(3.6)+0.056* 0-0.056* (204)/(3.6))/(0.331)\\\Rightarrow v_1=45.96844\ m/s`

The velocity of racket after hitting the ball is 45.96844 m/s