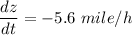Question

Ship A is 32 miles north of ship B and is sailing due south at 16 mph. Ship B is sailing due east at 12 mph. At what rate is the distance between them changing at the end of 1 hour?

Answer 1

`(dz)/(dt) =-5.6\ mile/h`

Step-by-step explanation:

distance between ship A and B = 32 mile

Ship A velocity in south, dx/dt = -16 mph

Ship B is sailing toward east with speed, dy/st = 12 mph

time = 1 hour

rate of change of distance between them = ?

x be the distance travel after t time

X = 32 + x

Let distance between them be z

now, using Pythagoras theorem to calculate distance between ships after 1 hours

z² = x² + y²

z² = (32 + x)² + 12²

z² = (32 - 16)² + 12²

z = √400

z = 20 miles

now, calculation of rate of change of distnace

z² = (32 + x)² + y²

differentiating both side w.r.t. time

`2 z (dz)/(dt) = 2(32+x)(dx)/(dt) + 2 y(dy)/(dt)`

`z (dz)/(dt) =(32-16)(dx)/(dt) +y(dy)/(dt)`

`20* (dz)/(dt) =16* (-16) +12* 12`

`(dz)/(dt) =(-112)/(20)`

`(dz)/(dt) =-5.6\ mile/h`

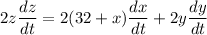
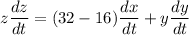
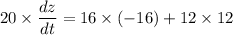
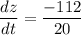
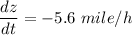
hence, the rate is the distance between them changing at the end of 1 hour is equal to
`(dz)/(dt) =-5.6\ mile/h`