Question

A machine has 12 identical components which function independently. The probability that a component will fail is 0.2. The machine will stop working if more than three components fail. Find the probability that the machine will stop working. A) 0.073 B) 0.795 C) 0.867 D)0.205

Answer 1

Answer: D)0.205

Explanation:

In binomial distribution, the probability of getting success in x trials is given by :-

`P(X=x)=^nC_xp^x(1-p)^(n-x)`

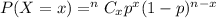
, where n is the total number of trials , p is the probability of getting success in each trial .

Given : The probability that a component will fail is 0.2.

Let x be the number of components will stop working.

i.e. p=0.2

n=12

Since The machine will stop working if more than three components fail.

Then, the probability that the machine will stop working will be :-

`P(X>3)=1-P(X\leq3)\\\\=1-[P(0)+P(1)+P(2)+P(3)]`

`=1-[^(12)C_0(0.2)^0(0.8)^(12)+^(12)C_1(0.2)^1(0.8)^(11)+^(12)C_2(0.2)^2(0.8)^(10)+^(12)C_3(0.2)^3(0.8)^(9)]`

`=1-[(1)(0.8)^(12)+(12)(0.2)(0.8)^(11)+(12!)/(2!10!)(0.2)^2(0.8)^(10)+(12!)/(3!9!)(0.2)^3(0.8)^(9)]\\\\=1-(0.068719476736+0.206158430208+0.283467841536+0.23622320128 )\\\\=1-0.79456894976\\\\=0.20543105024\approx0.205`

Hence, the probability that the machine will stop working is 0.205.

Thus , the correct answer is D)0.205