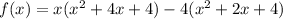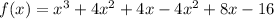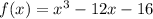Question

form a polynomial function whose real zeros are -2 with multiplicity 2 and 4 with multiplicity 1 whose degree is 3

Answer 1

`f(x) = {x}^(3) -12x - 16`

Explanation:

We want to for a polynomial function whose real zeros are -2 with multiplicity 2 and 4 with multiplicity 1.

If -2 is a zero of a polynomial, then by the factor theorem, x+2 is a factor.

Since -2 has multiplicity 2, (x+2)² is a factor.

Also 4 is a zero which means x-4 is a factor.

We write the polynomial in factored form as:

`f(x) = {(x + 2)}^(2) (x - 4)`

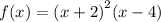
We expand to get:

`f(x) = ({x}^(2) + 4x + 4)(x - 4)`

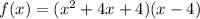
We expand further to get:

`f(x)=x({x}^(2) + 4x + 4) - 4({x}^(2) + 2x + 4)`

`f(x) = {x}^(3) + 4 {x}^2 + 4x - 4 {x}^(2) + 8x - 16`

`f(x) = {x}^(3) - 12x - 16`