Answer:
Part 1) AJ drawn the parabola opening upwards, instead of drawing it opening downwards
Part 2) see the explanation
Explanation:
Part 1) What mistake did AJ make in the graph?
we have
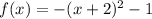
This is the equation of a vertical parabola written in vertex form
The parabola open downward (because the leading coefficient is negative)
The vertex represent a maximum
The vertex is the point (-2,-1)
therefore
AJ drawn the parabola opening upwards, instead of drawing it opening downwards
Part 2) Evaluate any two x-values (between -5 and 5) into AJ's function. Show your work. How does your work prove that AJ made a mistake in the graph?
take the values x=-4 and x=4
For x=-4
substitute the value of x in the quadratic equation
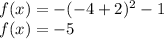
For x=4
substitute the value of x in the quadratic equation
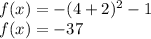
According to AJ's graph for the value of x=-4 the function should be positive, however it is negative and for the value of x=4 the function should be positive and the function is negative
therefore
AJ made a mistake in the graph