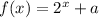Question

What function equation is represented by the graph?

f(x)=−2x−3

f(x)=−2x−2

f(x)=2x−3

f(x)=2x−2

Answer 1

`f(x)=2^x - 3`

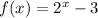
Explanation:

The choices are all exponentials, the x is raised to a power.

First of all, an exponential in the form:

`f(x)=a^x`

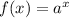
Where (a > 1)

Would have this shape and it will go through (0,1)

Now, looking at the graph, we see that it is translated 3 units down from (0,1).

The basic graph is
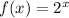`f(x)=2^x` and the translated one would be:

`f(x)=2^x - 3`

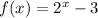
NOTE:

Basically is this is vertically translated a units down, the equation becomes:

`f(x)=2^x-a`

and if translated a units up, the equation would be:

`f(x)=2^x+a`