Final answer:
To find a vector of magnitude 3 in the direction of v = 4i - 3k, first calculate the unit vector by dividing v by its magnitude, and then multiply the unit vector by 3 to get the desired vector with magnitude 3.
Step-by-step explanation:
To find a vector of magnitude 3 in the direction of v = 4i - 3k, we must first find the unit vector in the direction of v. A unit vector has a magnitude of 1 and points in the same direction as the original vector. To find this unit vector, divide each component of v by its magnitude.
The magnitude of v is obtained using the formula
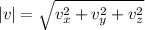 , where vx, vy, and vz are the components of the vector v. For the vector v = 4i - 3k, the magnitude is
, where vx, vy, and vz are the components of the vector v. For the vector v = 4i - 3k, the magnitude is
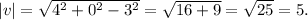
Next, the unit vector u in the direction of v is u = (1/|v|) * v = (1/5)(4i - 3k) = 0.8i - 0.6k.
To get the desired vector of magnitude 3, we multiply the unit vector by 3: 3u = 3(0.8i - 0.6k) = 2.4i - 1.8k. Thus, the vector 2.4i - 1.8k has a magnitude of 3 and is in the direction of the original vector v.