Question

point A is located at (2,6) and point B is located at (18,12) . what point partitions the directed line segment ab into a 2:3 ratio

Answer 1

(8.4, 8.4) or
`\left((42)/(5), (42)/(5)\right)`

Step-by-step explanation:

Given points are A(2, 6) and B(18, 12).

Let P(x, y) partitions the line segment in the ratio 2 : 3.

That is AP : PB = 2 : 3.

A(2, 6) can be taken as
`A(x_1, y_1).`

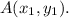
B(18, 12) can be taken as
`B(x_2, y_2).`

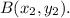
AP : PB can be taken as m : n = 2 : 3.

The coordinate of point P(x, y) divides line segment joining
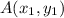`A(x_1, y_1)`and
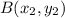`B(x_2, y_2)` in ratio m : n is

`P(x,y)=((mx_2+nx_1)/(m+n), (my_2+ny_1)/(m+n))`

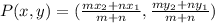
Here,
`x_1 = 2, x_2=18, y_1=6, y_2=12` and m = 2, n = 3.

Substitute these in the above formula, we get

`P\left(x, y\right)=\left((2 * 18+3 * 2)/(2+3), (2 *12+3 * 6)/(2+3)\right)`

`=\left((36+6)/(5), (24+18)/(5)\right)`

`=\left((42)/(5), (42)/(5)\right)`

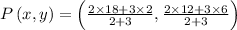
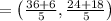
= (8.4, 8.4)

Hence, the point partitions the line segment is (8.4, 8.4) or
`\left((42)/(5), (42)/(5)\right)`.