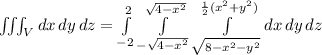Question

Set up the triple integral for the volume of the solid that is the common interior below the sphere x2+ y2+ z2= 8 and above the paraboloid z= 1/2 (x2+ y2)

Answer 1

`\iiint_V dx\,dy\,dz = \int\limits_(-2)^(2) \int\limits_(-√(4-x^2))^(√(4-x^2)) \int\limits_(√(8-x^2-y^2))^{(1)/(2)(x^2+y^2) } dx\,dy\,dz`

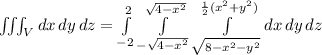
Explanation:

The common region enclosed above the paraboloid
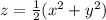`z = (1)/(2) (x^2+y^2)` and below the sphere
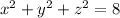`x^2 +y^2+z^2 = 8` is the solid.

Let's find the limit bounds for
`z`.

The region is bounded above by the sphere
`x^2 +y^2+z^2 =8` .

Isolate
`z` from the equation above.

`x^2 +y^2+z^2 = 8 \iff z^2 = 8 - x^2 +y^2 \implies z = √(8-x^2-y^2)`

On the other hand, the region is bounded below by the paraboloid
`z = (1)/(2) (x^2+y^2)`

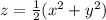
Therefore, we obtain

`√(8-x^2-y^2) \leq z \leq (1)/(2) (x^2+y^2)`

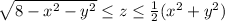
Now, we need to find the intersection of the sphere and the paraboloid. To do so, we need to solve the following system of equations

`x^2 +y^2+z^2 = 8`

`z = (1)/(2) (x+y) \implies 2z = x^2 + y^2`.

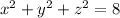
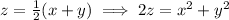Substitute the second equation in the first equation. We obtain

`2z+z^2 = 8 \implies (z-2)(z+4) = 0 \implies z = 2 \quad \vee \quad z = -4`

Hence, the paraboloid and the sphere intersect when
`z= 2`.

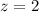Substituting
`2` for
`z` in the equation above gives

`x^2+y^2 = 4`

which is a circle with a radius
`2`.

Now, we can find the bond for
`x` and
`y`.

For
`y`, we obtain

`√(-4-x^2) \leq y \leq √(4-x^2)`.

For
`x`, we have

`-2 \leq x \leq 2`.

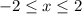Therefore, the needed triple integral is

`\iiint_V dx\,dy\,dz = \int\limits_(-2)^(2) \int\limits_(-√(4-x^2))^(√(4-x^2)) \int\limits_(√(8-x^2-y^2))^{(1)/(2)(x^2+y^2) } dx\,dy\,dz`