Question

Inarecentairlinedisaster,anairlinerflyingat30,000ft,550mi/h, lost power and fell to Earth. The mass of the aircraft was 255,000 lb. If the magnitude of the work done by drag force on the plane during the fall was 2.96 × 106 Btu, estimate the velocity of the aircraft at the time of impact, in mi/h. Let g = 32.08 ft/s2.

Answer 1

1413.7 mi/h

Step-by-step explanation:

height in air (H) = 30,000 ft = 30,000 x 0.3048 = 9,144 m

speed in air (v) = 550 mi/h = 550 x 0.44704 = 245.872 m/s

mass of aircraft = 255,000 lb = 255,000 x 0.453592 = 115666.054 kg

magnitude of the work done by drag force (W) = 2.96 × 10^6 Btu = 2.96 × 10^6 x 1055.06 = 3,122,977,600 J

acceleration due to gravity (g) = 32.08 ft/s^{2} = 32.08 x 0.3048 = 9.8 m/s^{2}

Take note that all values above are converted to their standard units

kinetic energy in air (KE1)= 0.5m
`v^(2)` = 0.5 x 115,666.054 x
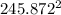`245.872^(2)` = 3,496,182,316.8 J

potential energy in air (PE1) = mgh = 115,666.054 x 9.8 x 9,144 = 10,364,973,898.2 J

potential energy on the ground (PE2) = 0 since height (h) is 0

from the energy balance equation KE2 + PE2 = KE1 + PE1 - W

where KE2 = kinetic energy on the ground and PE2 = 0

we now have KE2 = KE1 + PE1 - W

substituting all values into the equation above we have

KE2 = 3,496,182,316.8 + 10,364,973,898.2 - 3,122,977,600

KE2 = 10738178615 J

recall that kinetic energy = 0.5m
`v^(2)` , hence

10738178615 = 0.5 x 115666.054
`v^(2)`

`v^(2)` =
`(10738178615)/(0.5 x 115666.054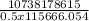)` = 185675.5

v=
`√(185675.5)`

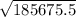
v = 430.9 m/s = 430.9 x 3.28084 = 1413.7 mi/h