Question

The lifetime of a 2-volt non-rechargeable battery in constant use has a Normal distribution with a mean of 516 hours and a standard deviation of 20 hours. The proportion of batteries with lifetimes exceeding 520 hours is approximately

A. 0.4207
B. 0.2000
C. 0.5793

Answer 1

Answer: A. 0.4207

Explanation:

Given : The lifetime of a 2-volt non-rechargeable battery in constant use has a Normal distribution with a mean of 516 hours and a standard deviation of 20 hours.

i.e.
`\mu=516`

`\sigma=20`

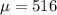
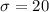
Let x denotes the lifetime of a 2-volt non-rechargeable battery in constant use.

Then , the probability of batteries with lifetimes exceeding 520 hours is approximately:-

`P(X>520)=1-P(x\leq520)\\\\=1-P((x-\mu)/(\sigma)\leq(520-516)/(20))\\\\=1-P(z\leq0.2)\ \ [\because\ z=(x-\mu)/(\sigma)]\\\\ =1-0.5793\ \ [\text{By z-table}]\\\\=0.4207`

Hence, the proportion of batteries with lifetimes exceeding 520 hours is approximately 0.4207.

∴ Correct option is A. 0.4207