Answer:
Range = 115$
Standard Deviation = 43.76$
Variance = 1915.142$
Option A) The measures of variation are not very useful because when searching for a room, low prices, location, and good accommodations are more important than the amount of variation in the area.
Explanation:
We are given the data for prices in dollars for one night at different hotels in a certain region.
234, 160, 119, 131, 218, 207, 146, 141
Range:
Sorted data: 119, 131, 141, 146, 160, 207, 218, 234
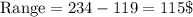
Standard Deviation:
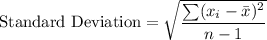
where
 are data points,
are data points,
 is the mean and n is the number of observations.
is the mean and n is the number of observations.

Sum of squares of differences = 4160.25 + 90.25 + 2550.25 + 1482.25 + 2352.25 + 1406.25 + 552.25 + 812.25 = 13406
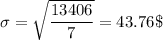
Variance =
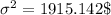
Measure of variance for someone searching for room:
Option A) The measures of variation are not very useful because when searching for a room, low prices, location, and good accommodations are more important than the amount of variation in the area.