Answer with explanation:
We can write the vectors such that:
v= 3i-1j
w= 1i+2j
v-w =3i-1j-1i-2j
X= v-w = 2i-3j = <2,-3>
2v= 2(3i-1j)=6i-2j
2v+w=6i-2j+1i+2j
Y = 2v+w= 7i = <7,0>
Unit vector in direction of v =
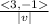
|v|=
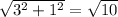
Unit vector in direction of v =

The sketches of v, w , v-w and 2v+w are attached.
In the graph Y is 2v+w and X is v-w