Question

A satellite is put in a circular orbit about Earth with a radius equal to 35% of the radius of the Moon's orbit. What is its period of revolution in lunar months? (A lunar month is the period of revolution of the Moon.)

Answer 1

0.21 lunar month

Step-by-step explanation:

the radius of moon = r₁

time period of the moon = T₁ = 1 lunar month

The radius of the satellite = 0.35 r₁

Time period of satellite

The relation between time period and radius

`T\ \alpha\ √(r^3)`

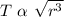
now,

`(T_2)/(T_1)=(√(r_2^3))/(√(r_1^3))`

`(T_2)/(T_1)=(√(0.35^3r_1^3))/(√(r_1^3))`

`(T_2)/(1)=√(0.35^3)`

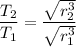
T₂ = 0.21 lunar month

hence, the time period of revolution of satellite is equal to 0.21 lunar month