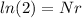Answer:
a)
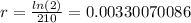
b)

Explanation:
For this case we assume the followin differential equation:
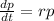
Where is is the consttant growth/decay rate , p represent the population and the the time.
For this case we can rewrite this expression like this:

And now we can apply integrals on both sides like this:
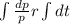
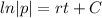
If we apply exponential on both sides we got:
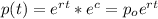
And from the previous equation
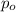 represent the initial population.
represent the initial population.
Part a
For this case we are assuming that the population doubles in t=210 so then we can set the following equation:
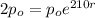
We can cancel
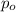 in both sides and we got:
in both sides and we got:
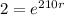
We can apply natural log on both sides and we got:
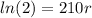
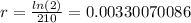
Part b
For this case we are assuming that the population doubles in t=N so then we can set the following equation:
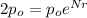
We can cancel
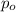 in both sides and we got:
in both sides and we got:
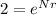
We can apply natural log on both sides and we got: