corrected question:
A rectangle and a square have the same perimeter. One side-length of the rectangle is 25% longer than the other. What is the ratio between the areas of the rectangle and the square?
Answer:
ratio of area of recatngle to square= 0.9879
Explanation:
perimeter of rectangle = 2(L+B)
perimeter of a square =
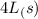
L=B+0.25B
L=1.25B
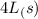 = 2(L+B)
= 2(L+B)
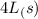 = 2(1.25B+B)
= 2(1.25B+B)
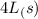 = 2(2.25B)
= 2(2.25B)
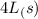 = 4.5B
= 4.5B
B= 4/4.5
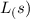
B= 0.889
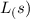 ..........equ1
..........equ1
area of square =

area of rectangle = L*B
=1.25B*B=

ratio of area of recatngle to square =

referring to equ 1
ratio of area of recatngle to square =
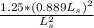
=

ratio of area of recatngle to square= 0.9879