Question

How many sequences of length 5 can be formed using the digits 0, 1, 2, . . . , 9 with the property that exactly two of the 10 digits appear, e.g., 05550

Answer 1

There are
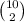`\binom{10}2` ways of picking any two digits.

The first digit can be chosen between 1 and 4 times; the remaining positions in the sequence are occupied by the other digit. The number of ways this can happen is

`\dbinom51\dbinom44+\dbinom52\dbinom33+\dbinom53\dbinom22+\dbinom54\dbinom11=\displaystyle\sum_(n=1)^4\binom5n`

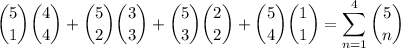
Then the total number of sequences that match the criterion is

`\displaystyle\binom{10}2\sum_(n=1)^5\binom5n=\boxed{1350}`

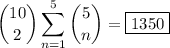
(where
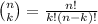`\binom nk=(n!)/(k!(n-k)!)`)