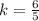Answer:
The constant of proportionality is
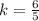
Explanation:
we know that
A relationship between two variables, x, and y, represent a proportional variation if it can be expressed in the form
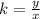 or
or
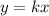
Let
x ----> the base of triangle
y ----> the height of triangle
To find out the constant of proportionality, divide the height by the base
First case
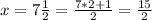
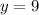
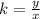
substitute
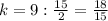
Simplify
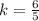
Second case
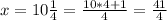
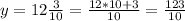
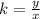
substitute
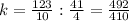
Simplify
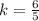
Third case
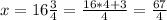
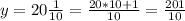
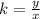
substitute
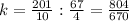
Simplify