Answer:
The graph has a domain of all real numbers.
The graph has a y-intercept at
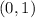 .
.
The graph has an x-intercept at
 .
.
Explanation:
Given: The graph is
![y=\sqrt[3]{x-1}+2](https://img.qammunity.org/2021/formulas/mathematics/high-school/48psh25h88eudgupsrlbihi68clc15xrph.png)
The domain of a function is a set of input values for which the function is real and defined.
Thus, the graph has a domain of
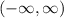 .
.
To find the y-intercept: To find the y-intercept, substitute
 in
in
![y=\sqrt[3]{x-1}+2](https://img.qammunity.org/2021/formulas/mathematics/high-school/48psh25h88eudgupsrlbihi68clc15xrph.png) .
.
![\begin{aligned}y &=\sqrt[3]{x-1}+2 \\&=\sqrt[3]{0-1}+2 \\&=-1+2 \\&=1\end{aligned}](https://img.qammunity.org/2021/formulas/mathematics/high-school/3hs79noib02nlllbevqw5cfnxopm216e96.png)
Thus, the y-intercept is
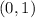
To find the x-intercept: To find the x-intercept, substitute
 in
in
![y=\sqrt[3]{x-1}+2](https://img.qammunity.org/2021/formulas/mathematics/high-school/48psh25h88eudgupsrlbihi68clc15xrph.png) .
.
![\begin{aligned}y &=\sqrt[3]{x-1}+2 \\0 &=\sqrt[3]{x-1}+2 \\-2 &=\sqrt[3]{x-1} \\(-2)^(3) &=(\sqrt[3]{x-1})^(3) \\-8 &=x-1 \\-7 &=x\end{aligned}](https://img.qammunity.org/2021/formulas/mathematics/high-school/ma7dnxphhzdfpsc1tqp0g0e2jwsvq7nfjr.png)
Thus, the x-intercept is
