Question

What is the period of the function f(x) = cos 2x?

A.) Pi/2
B.) 1/2
C.) Pi
D.) 2

Answer 1

C.) π

Explanation:

Given function:

`f(x)=cos(2x)`

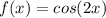
To find the period of the function.

Solution:

The general cosine function is given as:

`f(x)= A cos (Bx)`

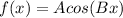
where
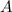`A` represents the amplitude of the function and the period of the function is given as:

⇒
`(2\pi)/(B)`

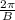
For the given function:
`f(x)=cos(2x)`

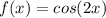
The period is given as:

⇒
`(2\pi)/(2)`

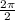
Cancelling the common terms, we have:

⇒
`\pi`

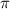
Thus, period of the given function = π