Consider the given function :
![{:\implies \quad \sf y=x\sqrt[3]{x}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tgc53orrm5f5sah06pakc10si3vq6n846v.png)
Before doing this question let's recall some basic formulae of calculus;
So, now let's move on to our question ;
![{:\implies \quad \sf y=x\sqrt[3]{x}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/tgc53orrm5f5sah06pakc10si3vq6n846v.png)
Can be further written as ;
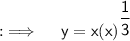
Using the 1st identity can be written as ;
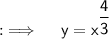
Now, differentiating both sides w.r.t.x ;
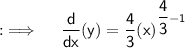
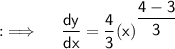
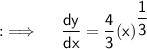
![{:\implies \quad \bf \therefore \quad \underline{\underline{(dy)/(dx)=(4)/(3)\sqrt[3]{x}}}}](https://img.qammunity.org/2023/formulas/mathematics/high-school/e1vvhd4z2jww0rk7gdhn6x677nmklxdc7t.png)
Hence, Option B) is correct