Question

As a sales person Jonathan is paid 50 per week +3% of the total Amount he sells. This week he wants to earn at least 100. Write an Inequality With Integer coefficients for the total sales needed to earn at least 100 describe what the solution represents.

Answer 1

The Inequality with integer coefficient for the total sales is
`5000+3x\geq 10000`

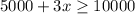
Hence Jonathan should make total sales of at least 1667 to earn at least 100.

Explanation:

Given:

Amount paid per week = 50

Addition amount = 3% of Total sales.

Let the Total sales be 'x'.

∴ Additional amount =
`(3)/(100)x`

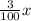
Amount he wants to earn this week
`\geq` 100

We need to write the inequality with integer coefficient for the total sales and also to find the total sales.

Solution:

We cans say that;

Amount paid per week plus Additional amount should be greater than or equal to Amount he wants to earn this week.

framing in equation form we get;

`50+(3)/(100)x\geq 100`

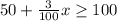
Now we will make the denominator common using LCM we get;

`(50*100)/(100)+(3)/(100)x\geq 100`

`(5000)/(100)+(3)/(100)x\geq 100`

`(5000+3x)/(100)\geq 100`

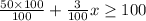
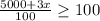
Multiplying both side by 100 we get;

`100 *(5000+3x)/(100)\geq 100* 100\\\\5000+3x\geq 10000`

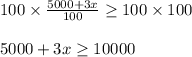
Hence The Inequality with integer coefficient for the total sales is
`5000+3x\geq 10000`

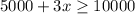
On solving the above equation we get;

Subtracting both side by 5000 we get;

`5000+3x-5000\geq 10000-5000\\\\3x\geq 5000`

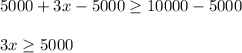
Dividing both side by 3 we get;

`(3x)/(3)\geq (5000)/(3)\\\\x\geq 1666.67`

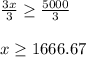
Hence Jonathan should make total sales of at least 1667 to earn at least 100.