Question

A quilt piece is designed with four congruent triangles to form a rhombus so that one of the diagonals is equal to the side length of the rhombus. Which measures are true for the quilt piece?

1. a = 60
2. x = 3 in.
3. The perimeter of the rhombus is 16 inches.
4. The measure of the greater interior angle of the rhombus is 90.
5. The length of the longer diagonal is approximately 7 inches.

Answer 1

1,3,5 are the answers hunny just finished the test

Explanation:

Answer 2

THE FOLLOWING MEASURES ARE TRUE FOR THE QUILT:

1. a = 60°

3. The perimeter of the rhombus is 16 inches.

5. The length of the longer diagonal is approximately 7 inches.

Explanation:

I have attached the picture describing the rhombus.

One by one we will check all the options:

As we can see that:

a+30°=90°

a = 90-30

1) a= 60° which is true

Taking the triangle with the perpendicular x, and using pythagoras theorem, we get:

`Perp^(2) +Base^(2) =Hyp^(2)`

`x^(2) +2^(2) =4^(2)`

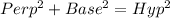
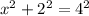
`x^(2)` =16-4 = 12

x=
`2√(3)`=3.46 ≠3

So option 2, is not true.

Perimeter of rhombus= 4 x 4 = 16 inches

So option 3 is correct

Smaller Interior angles of rhombus = 30+30= 60°

Measure of greater interior angle of rhombus = a+a=60+60 = 120°

So Option 4 is incorrect

The length of the longer diagonal is the horizontal diagonal which is:

x+x= 2x

2x= 2(3.46)=6.92 ≈ 7

So Option 5 is correct