Question

Two thin rods of length L are rotating with the same angular speed ω (in rad/s) about axes that pass perpendicularly through one end. Rod A is massless but has a particle of mass 0.76 kg attached to its free end. Rod B has a mass of 0.76 kg, which is distributed uniformly along its length. The length of each rod is 0.73 m, and the angular speed is 4.7 rad/s. Find the kinetic energies of rod A with its attached particle and of rod B.

Answer 1

Step-by-step explanation:

For rod A:

Length = 0.73 m

Mass of particle attached, m = 0.76 kg

Moment of inertia of this system about the given axis is as follows.

I =
`ml^(2)`

=
`0.76 kg * (0.73)^(2)`

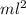
= 0.405
`kg m^(2)`

Angular speed of the rod (
`\omega`) = 4.7 rad/s

Now, the relation between kinetic energy, moment of inertia and angular speed is as follows.

K.E =
`(1)/(2) I \omega^(2)`

=
`(1)/(2) 0.405 kg m^(2) (4.7)^(2)`

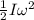
= 4.47 J

Therefore, kinetic energy of rod A is 4.47 J.

For rod B:

Length = 0.73 m

Mass of the rod, m = 0.76 kg

Moment of inertia will be as follows.

I =
`(1)/(3) ml^(2)`

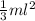
Putting the given values into the above formula as follows.

I =
`(1)/(3) ml^(2)`

=
`(1)/(3) * 0.76 kg (0.73)^(2)`

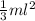
= 0.135
`kg m^(2)`

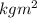
Angular speed is given as 4.7 rad/s. Therefore, calculate the value of kinetic energy as follows.

K.E =
`(1)/(2) I \omega^(2)`

=
`(1)/(2) * 0.135 * (5.7)^(2)`

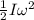
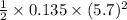
= 2.19 J

Hence, kinetic energy of rod B is 2.19 J.