Question

Bowling balls are roughly the same size, but come in a variety of weights. Given its official radius of roughly 0.110 m, calculate the heaviest bowling ball that will float in a fluid of density 1.100

Answer 1

To solve this problem we will apply the concepts related to the balance of forces. In this case the force caused by the weight and the buoyancy force on the Fluid. Both are forces that start from Newton's second law and can be expressed as

Weight

`F_W = mg`

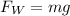
Here,

m = mass

g = Gravity

Buoyant Force

`F_B = \rho_(fluid)V_(pin)g`

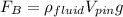
Here

`\rho_(fluid) =` Density of Fluid

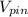`V_(pin)`=Volume

g = Gravity

By equilibrium we have that

`F_W = F_B`

`mg=\rho_(fluid)V_(pin)g`

`m=\rho_(fluid)V_(pin)`

`m=\rho_(fluid)((4)/(3) \pi r^3 )`

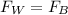
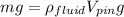
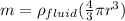
Replacing,

`m=(1.1*10^3) [(4/3)\pi(0.11)^3]`

`m =6.132 Kg`

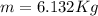
Now the Weight of the balls would be

`F = mg`

`F = 6.132 (9.8)`

`F = 60.0936N`

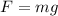
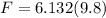
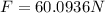
Therefore the heaviest bowling ball that will float in this fluid is 60.0936N