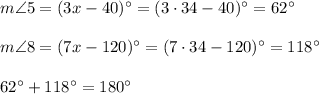Answer:
See explanation
Explanation:
16. Two parallel lines are cut by transversal. Angles with measures
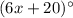 and
and
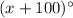 are alternate exterior angles. By alternate exterior angles, the measures of alternate exterior angles are the same:
are alternate exterior angles. By alternate exterior angles, the measures of alternate exterior angles are the same:
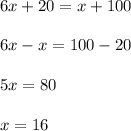
Then
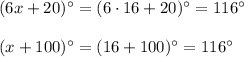
17. Two parallel lines are cut by transversal. Angles with measures
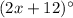 and
and
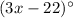 are alternate interior angles. By alternate interior angles, the measures of alternate interior angles are the same:
are alternate interior angles. By alternate interior angles, the measures of alternate interior angles are the same:
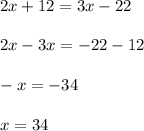
Then
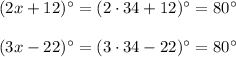
18. Two parallel lines are cut by transversal. Angles with measures
 and
and
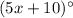 are alternate exterior angles. By alternate interior angles, the measures of alternate exterior angles are the same:
are alternate exterior angles. By alternate interior angles, the measures of alternate exterior angles are the same:
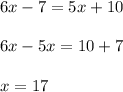
Then
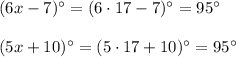
19. The diagram shows two complementary angles with measures
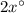 and
and
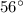 . The measures of complementary angles add up to
. The measures of complementary angles add up to
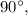 then
then
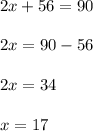
Hence,
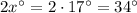
Check:
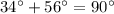
20. Angles
 and
and
 are vertical angles. By vertical angles theorem, vertical angles are congruent, so
are vertical angles. By vertical angles theorem, vertical angles are congruent, so
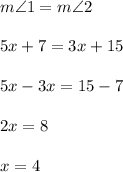
Hence,
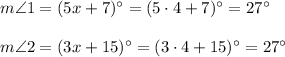
21.
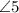 and
and
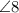 are supplementary. The measures of supplementary angles add up to
are supplementary. The measures of supplementary angles add up to
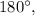 so
so
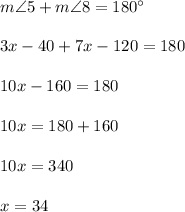
Therefore,