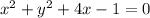Question

Find the equation of the circle with a diameter whose end points are (-1,-2) and (-3,2)

Answer 1

The equation of the circle with a diameter whose end points are (-1,-2) and (-3,2) is

`x^(2) +y^(2)+4x-1=0`

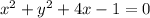
Step-by-step explanation:

Step-by-step explanation:-

Step 1:-

The equation of the circle having center and radius is

`(x-h)^2+(y-k)^2=r^2`

here center is (h,k) and radius is r

Given diameter whose end points are (-1,-2) and (-3,2)

The diameter of the circle is passing through the center of the circle

so center of the circle = midpoint of two end points

`((-1 +(-3) )/(2) ,(-2+2 )/(2)  )`

`(-2,0)`

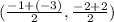
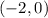
therefore center (h,k) = (-2,0)

Step 2:-

we have to find the radius of the circle

the radius of the circle = the distance from center to the one end point

i.e., C P = r

Given one end point is P(-3,2) and center C(-2,0)

The distance formula of two points are

`\sqrt{(x_(2)-x_(1) ) ^(2)+ (y_(2)-y_(1) ) ^(2)}`

`r=\sqrt{{(-3)-(-1) ) ^(2)+ (2-(-2)) ^(2)}`

`r=√(5)`

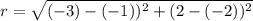
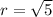
Step 3:-

center (h,k) = (-2,0) and

radius
`r=√(5)`

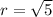
The standard form of circle equation

`(x-h)^2+(y-k)^2=r^2`

`(x-(-2))^2+(y-0)^2=√(5) ^2`

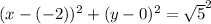
on simplification is

`x^(2) +y^(2)+4 x-1=0`