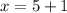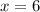Answer:
a) x = -7
b) x = -3/2
c) x = -3/2
d) x = 2
e) x = -1
f) x = -2
g) x = 7/3
h) z = -18/5
i) x = 6
Step-by-step explanation:
The are a couple of rules you should know first.
Negative exponent rule:
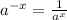
A negative exponent means the same thing as the positive exponent as a denominator under 1.
Exponent to another exponent:
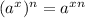
When raising an exponent to another exponent, you multiply the exponents.
Fraction as a base rule:
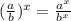
Apply the exponent to the numerator and denominator.
Base 1 rule:
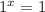
1 to the power of anything is 1.
Focus on exponents only:
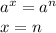
If the bases are the same on both sides of the equation, you can solve for "x" in the exponent by focusing on it only.
Write as an exponent: Rewrite a normal number as an exponent instead. Example:
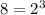 or
or
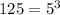
Also, you need to know how to rearrange and simplify formulas to isolate variables (by doing reverse operations in reverse BEDMAS order).
Know how to use the distributive property with brackets, when you multiply each of the terms in the brackets with the term on the outside.
Use each of these rules to solve.
a)
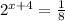 Write 8 as exponent
Write 8 as exponent
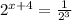 Negative exponent rule
Negative exponent rule
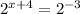 Focus on exponents only
Focus on exponents only
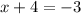 Subtract 4 from each side to isolate
Subtract 4 from each side to isolate
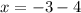
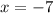
b)
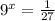 Write 27 as exponent
Write 27 as exponent
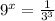 Write 9 as exponent
Write 9 as exponent
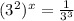 Exponent to another exponent
Exponent to another exponent
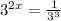 Negative exponent rule
Negative exponent rule
 Focus on exponents only
Focus on exponents only
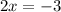 Divide both sides by 2 to isolate
Divide both sides by 2 to isolate
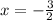
c)
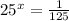 Rewrite 125 as exponent
Rewrite 125 as exponent
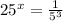 Rewrite 25 as exponent
Rewrite 25 as exponent
 Exponent to another exponent
Exponent to another exponent
 Negative exponent rule
Negative exponent rule
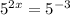 Focus only exponents only
Focus only exponents only
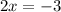 Divide both sides by 2 to isolate
Divide both sides by 2 to isolate
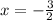
d)
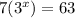 Divide both sides by 7 to isolate
Divide both sides by 7 to isolate
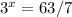
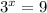 Write 9 as exponent
Write 9 as exponent
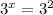 Focus on exponents
Focus on exponents

e)
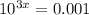 Write 0.001 as fraction
Write 0.001 as fraction
 Write 1/1000 as exponent
Write 1/1000 as exponent
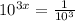 Neg. exponent
Neg. exponent
 Focus on exponents
Focus on exponents
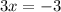 Divide both sides by -3
Divide both sides by -3
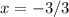
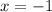
f)
 Divide both sides by 6
Divide both sides by 6
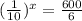
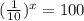 Write 100 as exponent
Write 100 as exponent
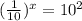 Fraction as base rule
Fraction as base rule
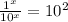 Base 1 rule
Base 1 rule
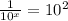 Neg. exponent
Neg. exponent
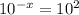 Focus on exponent
Focus on exponent
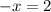 Divide both sides by -1
Divide both sides by -1

g)
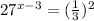 Write 27 as exponent
Write 27 as exponent
 Exponent to another exponent
Exponent to another exponent
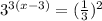 Fraction as base
Fraction as base
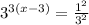 Base 1 rule
Base 1 rule
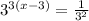 Neg. exponent
Neg. exponent
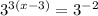 Focus
Focus
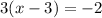 Distribute over brackets
Distribute over brackets
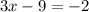 Add 9 to both sides
Add 9 to both sides
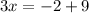
 Div. both sides by 3
Div. both sides by 3
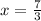
h)
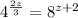 Write 4 as exponent
Write 4 as exponent
 Exponent to another exponent
Exponent to another exponent
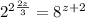 Write 8 as exponent
Write 8 as exponent
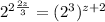 Exponent to another exponent
Exponent to another exponent
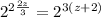 Focus
Focus
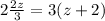 Multiply whole number with fraction
Multiply whole number with fraction
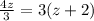 Distribute
Distribute
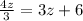 Multiply both sides by 3
Multiply both sides by 3
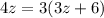 Distribute
Distribute
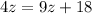 Subtract 9z from both sides
Subtract 9z from both sides

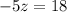 Div. both sides by -5
Div. both sides by -5
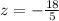
i)
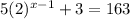 Subtract 3 on both sides
Subtract 3 on both sides
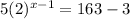
 Div. both sides by 5
Div. both sides by 5
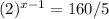
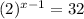 Write 32 as exponent
Write 32 as exponent
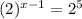 Focus
Focus
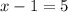 Add 1 to both sides
Add 1 to both sides