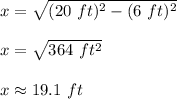Question

Brian borrowed a 20 foot extension ladder to use when he paints his house. If he sets the base of the ladder 6 feet from the house, as shown below, how far up will the top of the ladder reach? Round to one decimal place.

Answer 1

Step-by-step explanation:19.1 feet

Answer 2

Answer: 19.1 feet.

Explanation:

Draw a right triangle as the one shown attached, where "x" is the height in feet that the top of the ladder will reach.

You need to use the Pythagorean Theorem:

`a^2=b^2+c^2`

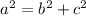
Where "a" is the hypotenuse and "b" and "c" are the legs of the right triangle.

If you solve for one of the legs, you get:

`a^2-b^2=c^2\\\\c=√(a^2-b^2)`

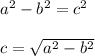
In this case, you can identify that:

`a=20\ ft\\b=6\ ft\\c=x`

Then, you can substitute values into the equation
`c^2=√(a^2-b^2)` :

`x=√((20\ ft^2)-(6\ ft)^2)`

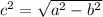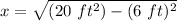
Finally, you must evaluate in order to find the value of "x".

Through this procedure, you get the following result:

`x=√((20\ ft)^2-(6\ ft)^2)\\\\x=√(364\ ft^2) \\\\x\approx19.1\ ft`