Answer:
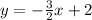
Explanation:
Assuming the question wants you to write and equation passing through (2,-1); and parallel to y=-3/2x+6.
Then we use the slope intercept form:

We substitute the point and slope to get:
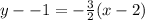
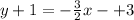

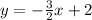
Note that parallel lines have the same gradient.