Answer:
![g^(-1)(x) = \sqrt[3]{(x - 5)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zucabgyp98yo0vovy2h4gav9gutbe2dp4u.png)
Explanation:
To find the inverse of a function, you can switch the "x" and "y" variables, then isolate "y", then change it back to function notation with the superscript ⁻¹.
You can't see "y" in the given function, but y = g(x). g(x) is the way you write "y" in function notation. The inverse function notation is g⁻¹(x).
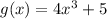
 Change "g(x)" to "y"
Change "g(x)" to "y"
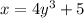 Switch the "x" and "y" variables
Switch the "x" and "y" variables
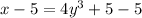 Subtract 5 from both sides to start isolating "y"
Subtract 5 from both sides to start isolating "y"
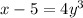 5 - 5 cancels out on right side
5 - 5 cancels out on right side
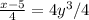 Divide both sides by 4
Divide both sides by 4
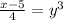 4y³/4 cancels out the 4 on the right side
4y³/4 cancels out the 4 on the right side
![\sqrt[3]{(x - 5)/(4)}= \sqrt[3]{y^(3)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/psjhrvonoca9mzwyfj06fcp8d1yxokrkl0.png) Cube root both sides
Cube root both sides
![\sqrt[3]{(x - 5)/(4)} = y](https://img.qammunity.org/2021/formulas/mathematics/middle-school/8mybyylk6yc87uq3lsa8g87ez537ysgdaa.png) ∛y³ cancels out the ³ on the right side
∛y³ cancels out the ³ on the right side
![y = \sqrt[3]{(x - 5)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/v54se0rhj5spw51ic9nn4nz2680u533zju.png) Variable on left side is standard formatting
Variable on left side is standard formatting
![g^(-1)(x) = \sqrt[3]{(x - 5)/(4)}](https://img.qammunity.org/2021/formulas/mathematics/middle-school/zucabgyp98yo0vovy2h4gav9gutbe2dp4u.png) Change the inverse function notation g⁻¹(x)
Change the inverse function notation g⁻¹(x)
The inverse of g(x) = 4x³ + 5 is g⁻¹(x) = ∛[(x-5)/4].