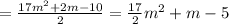Question

A rectangle with a perimeter of 19m^2+2m-10 and a width of m^2 write an expression for the lenght

Answer 1

Answer:
`(17)/(2)m^2+m-5`

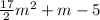
Explanation:

By definition, the perimeter of a rectangle is:

`P=2l+2w`

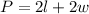
Where "l" is the lenght and "w" is the width.

If you solve for "l":

`P-2w=2l\\\\l=(P-2w)/(2)`

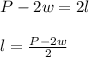
In this case, you know that the following expression represents the perimeter of the rectangle:

`19m^2+2m-10`

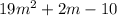
And the width of that rectanle is represented wih this expression:

`m^2`

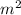
Therefore, based on the explained above, you can conclude that the lenght of that rectangle is given by:

`(19m^2+2m-10-2(m^2))/(2)`

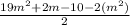
Finally, simplifying the expression, you get:

`=(17m^2+2m-10)/(2)=(17)/(2)m^2+m-5`