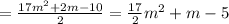Answer:
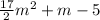
Explanation:
By definition, the perimeter of a rectangle is:
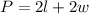
Where "l" is the lenght and "w" is the width.
If you solve for "l":
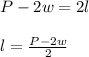
In this case, you know that the following expression represents the perimeter of the rectangle:
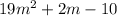
And the width of that rectanle is represented wih this expression:
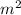
Therefore, based on the explained above, you can conclude that the lenght of that rectangle is given by:
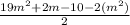
Finally, simplifying the expression, you get: