Question

Last weekend, she collected $283 from selling 8 bouquets and 6 table arrangements. The week before, she collected $491 from selling 10 bouquets and 12 table arrangements. What is the price of a table arrangement?

Answer 1

Price of a table arrangement = $30.5

Step-by-step explanation:

Let x be the bouquets and y be the table

Given:

she collected $283 from selling 8 bouquets and 6 table arrangements, so the equation is.

`8x+6y=283` ---------------(1)

The week before, she collected $491 from selling 10 bouquets and 12 table arrangements, so the second equation is written as.

`10x+12y=491` ------------------(2)

We need to find the price of a table arrangement.

Solution:

First we solve the equation 1 for x.

`8x+6y=283`

`8x=283-6y`

`x=(283-6y)/(8)`

Substitute x value in equation 2.

`10((283-6y)/(8))+10y=491`

Simplify

`(10* 283)/(8)-(10* 6y)/(8) + 12y = 491`

`(2830)/(8)-(60y)/(8)+12y=491`

Both fraction number divided by 2.

`(1415)/(4)-(30y)/(2)+12y=491`

`12y-(30y)/(4)=491-(1415)/(4)`

`(4* 12y-30y)/(4)=(4* 491-1415)/(4)`

`(48y-30y)/(4)=(1964-1415)/(4)`

Multiply by 4 both side

`4*(18y)/(4)=4* (549)/(4)`

`y=(549)/(18)`

Both numerator and denominator divided by 9.

`y=(61)/(2)`

`y=30.5`

Therefore, the price of a table arrangement is $30.5

Answer 2

The price of each table arrangement is $30.5

Explanation:

Given as :

The Amount collected from selling 8 bouquets and 6 table arrangement = $283

The Amount collected from selling 10 bouquets and 12 table arrangement = $491

Let The price of each bouquets = $b

Let The price of each table arrangement = $a

According the question

Number of bouquets sold × price of each bouquets + number of table arrangement sold × price of each table arrangement = Total amount collected

i.e 8 b + 6 a = $283 .......A

And

10 b + 12 a = $491 ............B

Now, Solving equation a and B

2 × (8 b + 6 a) - (10 b + 12 a) = 2 × 283 - 491

Or, 16 b + 12 a - 10 b - 12 a = 566 - 491

Or, (16 b - 10 b) + (12 a - 12 a) = 75

Or, 6 b + 0 = 75

∴ b =
`(75)/(6)`

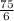
i.e b = $12.5

So, The price of each bouquets = b = $12.5

Put the value of b in eq A

∵ 8 b + 6 a = $283

i.e 8 × 12.5 + 6 a = $283

Or, $100 + 6 a = $283

Or, 6 a = $283 - $100

Or, 6 a = $183

∴ a =
`(183)/(6)`

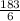
i.e a = $30.5

So, The price of each table arrangement = $30.5

Hence, The price of each table arrangement is $30.5 Answer