Question

Find the limit (enter 'DNE' if the limit does not exist)

Hint: rationalize the denominator.

lim(x,y)→(0,0)(−2x^2−6y^2)/sqrt(−2x^2−6y^2+1)-1

Answer 1

`\lim\limits_((x,y)\rightarrow(0,0))\left(√(-2x^2-6y^2+1)+1\right)=2`

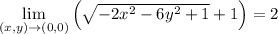
Explanation:

We need to first simplify the expression using rationalization(i.e. if a square root term exists in the denominator, then multiply and divide the whole expression by the denominator(but the change the sign of its middle term))

here, we need to find:

`\lim\limits_((x,y)\rightarrow(0,0))\left((-2x^2-6y^2)/(√(-2x^2-6y^2+1)-1)\right)`

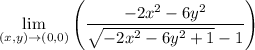
first we'll rationalize our expression:

`(-2x^2-6y^2)/(√(-2x^2-6y^2+1)-1)\left((√(-2x^2-6y^2+1)+1)/(√(-2x^2-6y^2+1)+1)\right)`

`(-(2x^2+6y^2)(√(-2x^2-6y^2+1)+1))/((√(-2x^2-6y^2+1)+1)^2-(1)^2)`

`(-(2x^2+6y^2)(√(-2x^2-6y^2+1)+1))/(-2x^2-6y^2+1-1)`

`(-(2x^2+6y^2)(√(-2x^2-6y^2+1)+1))/(-(2x^2+6y^2))`

`√(-2x^2-6y^2+1)+1`

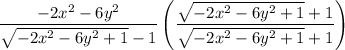
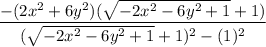
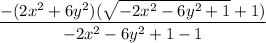
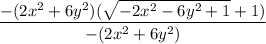
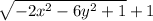
this is our simplified expression, now we can apply our limits:

`\lim\limits_((x,y)\rightarrow(0,0))\left(√(-2x^2-6y^2+1)+1\right)`

`√(-2(0)^2-6(0)^2+1)+1`

`1+1`

`2`

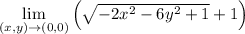
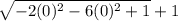
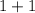
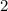
the limit does exists and it is 2.