Question

If a person drives 390 miles at an average of 40 miles per hour, then their distance d from the destination (in miles) is a function of the number of hours h driven.

Answer 1

`D(t) = 40 t`

Graph attached.

Explanation:

Assuming this complete problem:

"If a person drives 370 miles at 40 MPH then their distance d from the destination in miles is a function of the number of hours h driven

show equation graph and function"

We know from the definition of distance that
`D= vt`

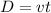
Where D represent the distance travelled on this case on mi, t the time in hours and v the velocity on this case in mi/h.

For this case if we want a function in terms of the time we can write this expression:

`D(t) = 40 t`

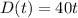
And since we know that the person travels 390 mi then we can find the total time spent on the travel like this:

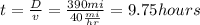`t = (D)/(v)= (390 mi)/(40 (mi)/(hr))=9.75 hours` approximately.

And the graph would be the figure attached,

Answer 2

Answer: d(h) = 390 - 40h

For h</= 9.75hours

Explanation:

Given;

Initial distance from the destination = 390miles

Average speed v = 40 miles/hour

Note; At time h= 0 their distance from the destination is maximum which is 390 miles. But as they move closer at constant speed their distance from the destination reduces at constant rate till it reaches zero (when they reach their destination)

d(0) = 390miles

d(t) = d(0) - constant rate(time)

d(t) = d(0) - vt. ......1

time taken to reach destination = d/v = 390/40 = 9.75 hours

Using equation 1, substituting v = 40miles/hour,

d(0) = 390 miles and at t = h

d(h) = 390 - 40h

For h</= 9.75hours