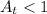Answer:
Explanation:
The given question incomplete; here is the complete question given in the attachment.
The rate of change of the mass A of salt at the time 't' is proportional to the square of the mass of salt present at the time t.
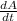 ∝ A²
∝ A²
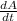 = kA² [k = proportionality constant]
= kA² [k = proportionality constant]
And the given conditions are
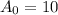 and
and

a).
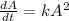
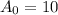 and
and

b). From the differential equation
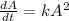
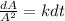
By integration on both the sides of the equation.

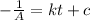 [c = integration constant]
[c = integration constant]
From the given conditions in the question,
For
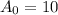 ,
,
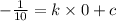
c =
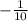
For
 ,
,
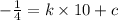
Since c =
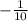
Therefore,
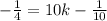
k =
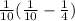
k =
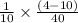
k = -

k = -
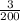
Now we place the values of constants in the solution of integration
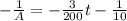
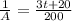
A =
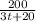
c). Now we have to calculate the time when A(t) < 1
From part b,
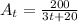
Therefore,
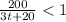
By solving the inequality,
3t + 20 > 200
3t > 200 - 20
3t > 180
t > 60
Therefore, after 60 hours