Question

(b) Use the right-hand rule to decide whether the components of a × b are positive, negative, or 0.

Answer 1

(a)

Given:

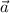`\vec{a}` is in xy plane and
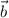`\vec{b}` is in the direction of k.

|a|=6 units, |b|=3 and θ = 90°

|a × b| = |a| × |b| sinθ

= |a| × |b| sin90°

= 6 × 3 × 1

|a × b| = 18

(b)

Let
`\vec{c}=\vec{a} * \vec{b}`

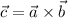
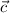`\vec{c}` is perpendicular to both
`\vec{a} \text { and } \vec{b}`.

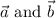In this case,

x-component of
`\vec{a} * \vec{b}` is positive.

y-component of
`\vec{a} * \vec{b}` is negative.

z-component of
`\vec{a} * \vec{b}` is zero.