Question

A uniform, solid cylinder of radius 5 cm and mass of 3 kg starts from rest at the top of an inclined plane that is 2 meters long and tilted at an angle of 25o with the horizontal, and the cylinder rolls without slipping down the ramp. Calculate the speed of the cylinder at the bottom of the ramp.

Answer 1

`v=3.33 m/s`

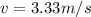
Step-by-step explanation:

We can use the conservation of energy here.

The solid cylinder has a gravitational energy at the top of the plane and kinetic energy at the end of the plane. Let's remember that the cylinder has kinetic energy due to the transnational movement and kinetic energy due to the rotational movement.

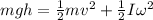`mgh=(1)/(2)mv^(2)+(1)/(2)I\omega^(2)` (1)

We know that ω=v/R and the moment of inertia around the central axis of a solid cylinder is I=(1/2)mR².

Now, we can rewrite (1) using the above definitions:

`mgh=(1)/(2)mv^(2)+(1)/(2)((1)/(2)mR^(2))((v)/(R))^(2)`

`mgh=(1)/(2)mv^(2)+(1)/(4)mv^(2)`

`mgh=(3)/(4)mv^(2)`

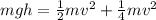
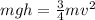
So we can solve it for v:

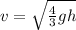`v=\sqrt{(4)/(3)gh}` (2)

Using the length and the angle we can find the height of the inclined plane.

`sin(\theta)=h/a`

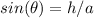
In our case:

• θ is 25°
• h is the height
• a is 2 meters

`h=a\cdot sin(\theta)=2sin(25)=0.85 m`

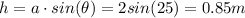
Finally, we put the value of h on (2) and find the speed next.

`v=\sqrt{(4)/(3)(gh)}=\sqrt{(4)/(3)(9.81*0.85)}`

`v=3.33 m/s`

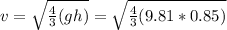
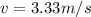
I hope it helps you!