Question

A light wave has a 670 {\rm nm} wavelength in air. Its wavelength in a transparent solid is420 {\rm nm} .a)What is the speed of light in this solid?b)What is the light's frequency in the solid?

Answer 1

Step-by-step explanation:

given,

Light wave wavelength in Air, λ_(vac) = 670 nm

wavelength in transparent solid, λ= 420 nm

Refractive index of the solid

`n = (\lambda_(vac))/(\lambda)`

`n = (670)/(420)`

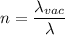
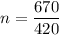
n = 1.6

a) speed of light in the solid

`v = (c)/(n)`

`v = (c)/(1.6)`

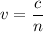
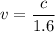
v = 0.625 c

b) light's frequency in the solid

`f = (c)/(\lambda_(vac))`

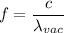
frequency of light remain same when light move from one medium to another.

f is the frequency of light

`f = (3* 10^8)/(670* 10^(-9))`

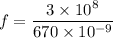
f = 4.47 x 10⁻¹⁴ Hz

the light's frequency in the solid is equal to 4.47 x 10⁻¹⁴ Hz