Answer: The boiling point of solution is 80.32°C
Step-by-step explanation:
To calculate the molality of solution, we use the equation:
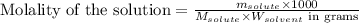
Where,
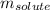 = Given mass of solute (eugenol) = 0.144 g
= Given mass of solute (eugenol) = 0.144 g
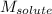 = Molar mass of solute (eugenol) = 164.2 g/mol
= Molar mass of solute (eugenol) = 164.2 g/mol
 = Mass of solvent (benzene) = 10.0 g
= Mass of solvent (benzene) = 10.0 g
Putting values in above equation, we get:

To calculate the elevation in boiling point, we use the equation:

where,
 = elevation in boiling point =
= elevation in boiling point =
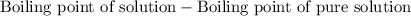
Boiling point of pure solution (benzene) = 80.1°C
i = Vant hoff factor = 1 (For non-electrolytes)
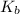 = molal boiling point elevation constant = 2.53°C/m
= molal boiling point elevation constant = 2.53°C/m
m = molality of solute = 0.088 m
Putting values in above equation, we get:
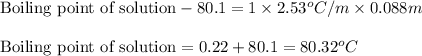
Hence, the boiling point of solution is 80.32°C